Linear Programming
Linear programming is the strongest method currently available that will work 'out of the box' on large optimisation problems. It is limited to a particular class of model, but there are theorems covering the nature of the solution and also an algorithm (the simplex algorithm) that apply to all well-posed optimisation problems in this class. While the restrictions on the type of model seem quite limiting, in practice it is found that by creative model building it is possible to cover a wide range of problems. The important advantage of linear programming is that the method can deal with hundreds of decision variables, and within this huge space identify and set the values of the variables that are critical in the problem. No other optimisation method can deal with such large problems.
Linear programming is so called because all the components of the problem are linear expressions of the decision variables, each of which is a single range of real numbers usually >=0. All expressions in the problem must be in the linear form:
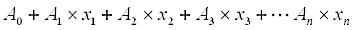
where xi are the decision variables and Ai are real constants which may be zero, positive or negative.
Typical optimisation problems which have been solved by linear programming are given in the following list. The list also indicates how often the LP models are run.
- Blending (for example margarine) - weekly;
- Production planning - quarterly;
- Oil refinery management - weekly;
- Distribution planning - daily;
- Financial planning - quarterly;
- Manpower planning - monthly;
- Blast furnace loading - daily;
Formulation of particular examples of these LP problems will have many constituents, but typical problems will include:
| Constituent | Example |
|---|---|
| Variables |
the quantities of products to be produced; processing hours used on machines; quantities of materials stored and purchased. |
| Constraints |
plant process capacity; material quantities available; materials required for products; amounts of products that can be sold |
| Cost Function |
Profit from sale of products; Cost of materials; Cost of running plant; |
The are LP solvers available in some spread sheets e.g. Excel. These are suitable for small one-off LP problems. However for larger commercial scale problems, which will be run regularly, a specialised LP package should be used. This will have a solver with superior numerical stability and capacity plus model building facilities which will support regular and methodical updating.
Creating and interpreting Linear Programming models requires experience. However once the model has been created and validated it can be rerun with different data with little effort.
Optimal Solutions welcomes enquiries on Linear Programming, and would be pleased to offer consultancy on this, or any other aspect of Optimisation. You can get in touch by sending a message from our Contact Us page, or by calling us on the number below.