Calculus and Gradient Search
For Calculus and Gradient search methods the modelA simplified description providing a basis for an empirical understanding and representation of a system that can be used to forecast its behaviour according to a set of decisions. and cost functionsA function that returns a value from a well ordered set for each of the outcomes from a set of decisions. The well ordered set is usually the set of all real number and the cost can often be interpreted in monetary terms.. are combined to form one unified function. Both these methods can be used when there are few and continuous decision variables and when the unified model is smooth and bounded within the region given by the constraints on the decision variables.
These methods rely on the fact that at a local maximum or minimum the gradient is zero. The same principle applies when there is more than one decision variable.
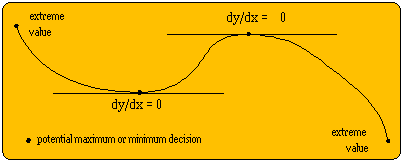
With the calculus method the unified cost function is differentiated, and the differentials are equated to zero and solved. The overall maximum or minimum can be identified by substituting the solutions into the unified cost function. More or less the same procedure is carried out along the constraints of the decision region (extreme values) and the overall maximum or minimum is determined. This method is an entirely mathematical exercise and is straightforward for a single decision variable, but can only be used if the unified function is differentiable. The method extends to more than one decision variable using partial differentials but may be much more difficult to apply.
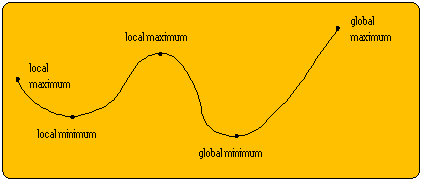
The gradient method is the numerical counterpart to the calculus method and is implemented within computer programs. It can be used when the unified function cannot be differentiated in closed form or the resulting equations cannot be solved. The gradient along each independent decision variable is determined either from the differentiated function or by the difference between adjacent points. The decision variable with the greatest gradient is selected and a the value adjusted by a step that is related to the gradient. The procedure is repeated until all gradients are sufficiently small. Because of the problem with local maxima and minima a number of starting positions must be tried, including starting points on the constraint boundaries. All local maxima and minima should be stored so that the overall maximum or minimum can be found.
There are no commercial tools for carrying out gradient search methods but the technique is relatively easy to code as module in most programming languages.
Optimal Solutions 4U can develop unified cost models, calculus solutions and gradient search modules in most programming languages. We would be pleased to offer consultancy on this, or any other aspect of Optimisation. You can get in touch by sending a message from our Contact Us page, or by calling us on the number below.